Delphi For Fun Newsletter #80
[Home]
April 4, 2016
Spring has "sprung", and rebounded back to winter a couple of times so far here on our mountain. The smart plants are holding back their blossoms for another week or two. The loggers have finished cutting 18 acres of our pines. The skidder and loader are still setting on the log deck waiting for their next job but the checks have all come in - with the wife's permission, there may be a sawmill in my future!
Looking at the 1st quarter projects, I see that programming projects predominate covering a wide range from Puzzles to Daylight Saving Time in the Southern Hemisphere, Graph searching forward and backward, Touchtone phone signal generation, drawing paneled cabinet doors, and tracking "Great Circle" routes. Here are the details:
---------------------------------------------------------------------------------
January 2, 2016:
 OK,
holidays are over; back on the diet and back to "work", programming. Being
known to the family as a puzzle lover, I received one called "Aristotle's Number
Puzzle" for Christmas this year - nothing to do with Aristotle as far as I can
tell. It's a hexagon shaped board made up of of 19 hexagon shaped tiles numbered
1 through 19. The objective is to arrange them into a "magic" hexagon in
which values in every horizontal and diagonal row (15 in all) sum to 38.
Our "Brute Force" program can
find the 12 variations of the solution by defining 15 equations representing
sums for the 19 variables . These are all isomorphic versions of the single
solution, i.e. they represent rotations and mirroring of the solution. I decided
to investigate further, starting by posting a Delphi Techniques program to draw
Hexagonal Boards of
various sizes. Here's one with puzzle hints filled in.
OK,
holidays are over; back on the diet and back to "work", programming. Being
known to the family as a puzzle lover, I received one called "Aristotle's Number
Puzzle" for Christmas this year - nothing to do with Aristotle as far as I can
tell. It's a hexagon shaped board made up of of 19 hexagon shaped tiles numbered
1 through 19. The objective is to arrange them into a "magic" hexagon in
which values in every horizontal and diagonal row (15 in all) sum to 38.
Our "Brute Force" program can
find the 12 variations of the solution by defining 15 equations representing
sums for the 19 variables . These are all isomorphic versions of the single
solution, i.e. they represent rotations and mirroring of the solution. I decided
to investigate further, starting by posting a Delphi Techniques program to draw
Hexagonal Boards of
various sizes. Here's one with puzzle hints filled in.
January 20, 2016:
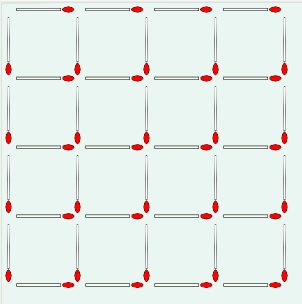
There are 30 squares of all sizes in a 4x4 grid of 40 matchsticks. "What is the minimum number of matchsticks that need to be removed to leave no squares of any size?"
How many Squares? investigates this problem, from the latest addition to my library of math & puzzle books: Challenging Math Problems, Terry Stickels, Dover Publications, 2015.
Program users can investigate various grid sizes and work on solving by
clicking to add or remove matchsticks with feedback along the way.
For those with a little mathematical curiosity, there are some interesting
relationships across grid sizes among the number of matchsticks, the number of
squares, and the minimum number of sticks to eliminate .
January 28, 2016: It did not take long to recognize the need for for the first two enhancements in last week's "How Many Squares" program. HowManySquares Version 2 adds the ability to view remaining squares after each move or on request. Also grids can now be saved and restored. Both features are helpful when working on larger grids. So far I've solved (and saved) up 7x7 grids. Still working on 8x8.
February 10, 2016:
Sound Generator is a program which can create complex tones by combining
multiple frequencies. Sound Generator
Version 3.0 uploaded today adds an option to easily create the
"Touch-Tone" sounds used in modern landline telephone connecting protocols.
The technology referred to as Dual Tone Multi-Frequency, DTMF, encoding. It
combines two frequencies to create 16 distinct tones for digits '0'
through '9', letters 'A' through 'D', plus '*' and '#'
special characters as illustrated in this grid at right. Multiple
characters in a string may be played and saved in a "wave" audio format
file. This may prove useful for testing a future program decoding audio tones back
to characters.
February 14, 2016: Aussies always like to break the mold and do things differently. They did it again with Daylight Saving Time (DST) calculations: Time Zone Demo Version 2.1 fixes two problems uncovered by a Brisbane programmer when he reported the demo program crashing. Problems when DST starts and ends in different years or regions with no DST at all (like Brisbane!) should be fixed. The program now reports correct end dates for Southern Hemisphere regions and "no DST for this location" instead of crashing when there is none. Changes have not been tested, but someone down under will surely let me know if the problems still existJ.
February 20, 2016:

Coal to Diamonds is a wicked hard puzzle to solve. "Coal"
is changed to "Diamond" in a thee step process. Each click of a cell of a 3x3
grid advances all elements in that row and column by one step. A high school student learning Java (L)
had a version of this puzzle in a coding competition except the goal was all
coal instead of all diamonds ([000 000 000] instead of [333 333
333]). I cleaned up some of the screen formats and text and added
user control of the goal state in Coal to
Diamonds Version 2.0.
February 21, 2016: For programmers - I wrote a Countdown timer control several years ago because I needed one for a puzzle program with a time limit. I later modified it to also "count up" in order to time long-running programs. I just added an "TimerPop" event exit to let the calling program check once per second to take any desired action based on run time or time remaining. The control is included with Countdown Demo Version 2.1 which now tests the feature by beeping once per minute.
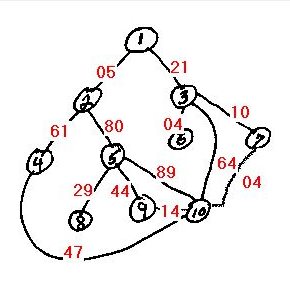 |
|
Shortest 2 to 10 path: |
March 3, 2016: Graph searching is a powerful tool for solving problems which move from state to state as it is solved. Think of a graph as a bunch of nodes (points) connected by edges (lines). These might be cities connected by roads or house connected by water lines, etc. where finding shortest paths might have real value. Most board games and puzzles are can also be represented by graphs where nodes are board states and edges are the moves that get from one board state to the next. For example, the February 20 "Coal to Diamonds" puzzle above can be the initial node with nine edges running to the 9 boards (nodes) resulting from clicking on each of the 9 squares. Each of those in turn will have up to 9 new edges as the next possible moves, etc. Eventually, there will be an all diamonds board (the solution) and the search objective is to find the shortest path from node to node which connects the initial board with the goal board.
The original demo illustrating the Dijkstra algorithm (method) for finding
shortest paths, calculated the shortest path from Node 1 to node 10 of a
sample graph using random weights (distances) from node to node. The search
was one-way (i.e. could only move to higher numbered nodes), but a programmer recently modified the program to search from
node 2 to node 10. A problem surfaced when the search failed because
then shortest path happened to be
2-1-3-7-10 which required traveling backwards through node 1. Shortest
Path Demo Version 2.0 posted today incorporates two-way searching and
allows users to specify both the start node and the goal node.
March 18, 2016:

An intermediate level exercise posted in our Delphi_Techniques code section
based on a a user's request for help drawing doors subdivided with one or
more vertical frames separated and divided by mullions of a given width and
position. Find out more and download source and executable file at
DrawingDoorFrames.
March 25, 2016: I first posted a program to calculate the distance between two points on the earth's surface in 2004. Distance is understood to be the shortest distance which is slightly mind-blowing when the Great Circle Route says that if you fly from New York to London, you must fly north over Newfoundland first ! Except at the equator, the shortest path to a location directly East of you involves starting out in a Northerly or Southerly (Southern hemisphere) direction and arrive traveling slightly South (or North).
Latitude Longiitude Distance Version 3.0 posted today is in response to a request from a blind(!) Delphi programmer working on a program that will allow other blind people to follow Great Circle routes from point to point and "explore" where they travel along the way. To do this Stefan needed a way to plot the bearings at steps along route. Version 3.0 does that by displaying points traversed when moving from given a starting bearing and a total distance. User can select 1, 10, or 100 steps and see the coordinates and the new bearings at each step along the way. I wish him the best in adapting this code to his application.
In the process, I uncovered an occasional "final bearing" error in my previous implementation of the algorithm which finds points from distances and directions. I made, and now use, a conversion of a National Geographic Information System (NGIS) Fortran program which is not only simpler, but eliminates the error.
Quotes redo (continued):
DFF News #9, December 1, 2000: If one is master of one thing and understands one thing well, one has at the same time gained insight into, and understanding of, many things." -- Vincent Van Gogh
DFF News #10, December 15, 2000:One accurate measurement is worth a thousand expert opinions" Admiral Grace Hooper (early computer pioneer, first to use the word "bug" to describe a programming error"
DFF News #11, January 14, 2001: "Hitch your wagon to a star." -- Ralph Waldo Emerson
DFF News
#12, February 6, 2001:
"Never stay up on the barren heights
of cleverness, but come down into the green valleys of
silliness." Ludwig Wittgenstein
(1889-1951), Austrian philosopher.
Click to subscribe or unsubscribe or to provide Feedback.
342,000 site visits and 366,400 program downloads in the past 12 months!