
Search

As of October, 2016, Embarcadero is offering a free release
of Delphi (Delphi
10.1 Berlin Starter Edition ). There
are a few restrictions, but it is a welcome step toward making
more programmers aware of the joys of Delphi. They do say
"Offer may be withdrawn at any time", so don't delay if you want
to check it out. Please use the
feedback link to let
me know if the link stops working.

Support DFF - Shop
If you shop at Amazon anyway, consider
using this link.
We receive a few cents from each
purchase. Thanks

Support DFF - Donate
If you benefit from the website, in terms of
knowledge, entertainment value, or something otherwise useful,
consider making a donation via PayPal to help defray the
costs. (No PayPal account necessary to donate via credit
card.) Transaction is secure.

Mensa®
Daily Puzzlers
For over 15 years
Mensa Page-A-Day calendars have provided several puzzles a year
for my programming pleasure. Coding "solvers" is most fun,
but many programs also allow user solving, convenient for "fill
in the blanks" type. Below are Amazon links to the
two most recent years.
Mensa®
365 Puzzlers Calendar 2017
Mensa®
365 Puzzlers Calendar 2018

(Hint: If you can
wait, current year calendars are usually on sale in January.)

Contact
Feedback:
Send an
e-mail with your comments about this program (or anything else).

|
| |
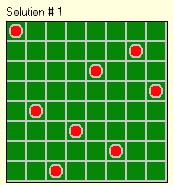
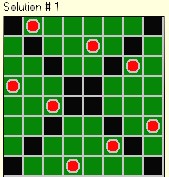
Problem Description
|
|
|
|
Traditional |
Plus (exclude diagonals) |
This is an extension of the "Eight Queens" problem: "Place 8
queens on a chessboard so that no queen threatens another". In this version we add the
restriction "and no queen lies on either main
diagonal".
In a single turn a queen can move multiple squares in a
straight line horizontally, vertically, or diagonally. So the problem may be rephrased as "place 8 markers
on a standard chess board so that no two are in line horizontally, vertically or
diagonally and no marker lies on either of the two main diagonals.
Background & Techniques
This is a classic example of a problem that can be solved with a
technique known as "graph searching" or "path finding", with
backtracking.
We start placing queens on the board in some
systematic manner and for each trial placement, check to see that no other queen
is in the same row, column or diagonal. If there is a conflicting
queen, retract the move in some manner that will prevent us from trying it again
and try the next location. If there is no conflicting queen, try
placing the next. If we run out of places to try, we have to notify the
previous queen that she is in the wrong place, etc. Eventually we will
either place all eight queens and succeed or will have tried all locations and
conclude that there is no solution.
Sometimes "rules of thumb" or heuristics can dramatically reduce
the search space and make such problems solvable (see "The Knights
Tour" for example). In this problem, the brute force method works fine to find a single
solution, although it may not find all solutions.
I've loaded 3 versions of this program, because that's the way the program evolved.
Version 1 solves the basic puzzle. Version 2 finds
multiple solutions by stepping through the grid and finding a solution for each
valid starting position (48 solutions = 64 squares minus the 16 diagonal
positions). One solution is returned each time the user presses the Solve button. Note that some are duplicates and others
represent
rotations or mirror images. Also note that there is no guarantee that we will find all solutions this way since there may
be multiple
solutions that have the same starting position.
In fact, I believe that there are only 2 unique solutions of the
"Plus" version, each with 8
variations
for a total of 16. The traditional version of the puzzle has 92 solutions
of which 12 are unique. These can also be displayed with their rotations and mirror
images. Version 3 identifies and displays these reversed and rotated images. It also
adds an OnDrawCell exit to the StringGrid to make a graphic display and
adds a user play facility.
PlaceCounter(n) in the recursively called function which looks for a place to
position the nth counter. A search is
made for a candidate square in the Board array, indicated by a 0
value. Three functions test whether the candidate's row, column, and
diagonals are unoccupied. If so, the value n is placed at that
location and if n is less than 8, we call ourselves with a value of n+1.
If no square can be found for queen n, we return false. A false
return triggers a reversion to the previous board at the previous level and we
continue searching.
Addendum May 1, 2002: I recently
received a feedback message from a viewer asking if would be possible to
cover a chessboard with 8 solutions to the original Eight Queens
problem (with main diagonals included). Not
knowing the answer, I wrote a little program to find out. (the
answer is no. Of the 92 solutions, 6 at most can co-exist on the
board. ) The really interesting part was implementing
Niklaus Wirth's algorithm for solving the problem. Wirth,
inventor of Delphi's ancestor, Pascal, came up with a most ingenious
technique: He used three small boolean arrays,
 | one with 8 members with False set when the row
corresponding to that entry is occupied, |
 | One with 15 members indexed from 2 to 16 with False entries
when the corresponding sum of a column and
row is occupied, These correspond to the top-right to
bottom-left diagonals (for example locations (1,4), (2,3),
(3,2), and (4,1) all fall on the same diagonal of that type,
represented by ColPlusRow[5]. |
 | And an array with 15 members indexed from -7 to +7
with False entries when the corresponding difference
of a column and row is occupied. These of course
represent the 15 top-left to bottom-right
diagonals. |
So for any column we now have an easy way check whether
diagonals are empty for any given column and row. Here's the recursive
depth first Search procedure that finds all 92 solutions:
procedure TForm1.Search (column: integer);
var
row: integer;
rowFlag,plusFlag,minusFlag: Boolean;
begin
for row := 1 to 8 do
begin
rowFlag := gRow[row];
plusFlag := ColPlusRow[column + row];
minusFlag := ColMinusRow[column - row];
if rowFlag and plusFlag and minusFlag then
begin
Solution[column] := row;
SetQueen(row, column);
if column < 8 then Search(column + 1)
else ShowSolution;
RemoveQueen(row, column);
end;
end;
end; {Search}
Procedure SetQueen sets the 3 array positions we just checked to False
and RemoveQueen sets the 3 array positions to True.
The Solution field ends up with 8 numbers corresponding to
the row numbers for each column.
A second button recursively searches solutions derived as above and tracks the
maximum number that can co-exist without overlapping. Best solution is
displayed as found.
It's not very polished or documented, but here is a link that will
download the source code for EightQueens_Wirth
if anyone is interested.
Addendum April 8, 2003: I cleaned up Eight Queens Wirth
today and added code to answer one more viewer's question "What is
the smallest set of solutions which will completely cover the
board?" My answer is 12, but I cannot prove it.
Viewers are invited to let me
know if you know of a smaller set.
Running/Exploring Eight Queens Wirth
|
Addendum December 27, 2004: While answering a viewer's question
recently, I had a chance to review the original Eight Queens code posted here 3
years ago and realized that the traditional version of the puzzle was not
included. I modified the 3 versions today to allow users to select whether
or not a queen can sit on a diagonal. So the Plus 3 version will now
display not only two unique solutions for the "Plus" version but also
the 12 unique solutions for the traditional version of the puzzle.
Each solution has 7 additional variations (rotations and mirrors) which are also
displayed. How does 8 versions of 12 unique solutions square with
the 92 solutions found by Eight Queens Wirth and others? It turns out that
solution #8 is unchanged after 180 degree rotation, so there are only 4 unique
versions of this solution, reducing the total potentially unique solutions from
96 to 92.
Running/Exploring Eight Queens Plus
Suggestions for Further Explorations
 |
December,
2004 Done: If you remove the initialization
of the diagonals
to -1 in InitBoard, you can find solutions for the original version of the
problem. I tried it and found 88 total and 11 unique
solutions. Searching the Web, I've found sites that say that there are 92
solutions with 12 unique. So there probably are cases where multiple
solutions have the same starting position. Niklaus Wirth, the originator of Delphi's
predecessor, Pascal, has published an optimized search algorithm for all
solutions that is available online. If I had
known about it before starting, it would probably be incorporated here. I
didn't, so it's up to you for now. |
 |
Search the Internet for Eight Queens
and you will turn up lots of sites with more good information. You could modify this
program to solve the N x N problem, perhaps find the maximum number of queens
that can be placed on an N x N board without capture. Is there a
way to find the
total number of solutions for a given size board without finding all the
solutions? |
| Originally posted: 12/13/2001 |
Modified:
05/15/2018
|
|

