A simulation program for an aircraft instrument simulator called the Horizontal Situation Indicator
is under development here at DFF. This Wind Triangle program was
written to make sure that I understood the concepts and mathematics for
navigating an aircraft in the desired
direction.
Objects moving though still air generally move in the direction they are pointed. However
moving air, i.e. the wind, will alter the course and speed of the object relative to the ground depending on the wind direction and speed.
Correcting for the wind is a necessary skill for airplane pilots, expert marksmen, and
successful golfers. Only airplanes generally fly slow enough and high enough that mathematically calculating the wind correction angle is worthwhile. The
technique uses "vector addition". Vectors are line segments that have a specific
direction, i.e. they are defined by a length and an angle. In our Wind Triangle we'll have three vectors:
Note that speeds substitute for distances here which is OK since they are
directly proportional. Under constant input conditions, whether you fly
for one minute or one hour, the distances traveled will be in proportion to the
speeds and the triangle will have exactly this same shape whichever
variable is plotted.
 |
|
WTA=Wind to
track Angle
WCA= Wind
Correction Angle |
In most cases, we want the Course to be an input and calculate the proper heading into the wind to offset its effect.
Search the web for "Plot Wind Triangle" and you will find a number of pages describing the geometric construction
technique.
This program provides an interactive version that uses trigonometry to determine the Heading that will
keep us on the desired Course. Playing with it will help develop an understanding of how the variables interact. A summary
of the equations used is given for each output.
:
The Equations
We are given 4 values as input. (Wind direction, Wind
speed, Airspeed and Desired Course Angle). This is the
minimum required to define the triangle and orient it in relative to
North. Here are the essential equations used to calculate the
missing parameters for our Wind Triangle: .
Wind Direction Adjustment
WindDir = Input WindDirection +180°
Since Wind directions are given as "From"
direction rather than "To", we'll add 180 degrees to get our vector
point in the correct (downwind) direction..
Wind To Track Angle:
WTAngle = DesiredCourse - WindDir
The input angles Wind direction (WinDir) and Desired Course (DesiredCourse)
are fixed angles independent of any other values. The difference is
calculated as a convenience in references in the equations below.
Wind Correction Angle
SinWca:=windspeed*sin(WTAngle)/Airspeed;
WCA:=arcSin(sinwca);
We'll define the Wind Correction Angle (WCA) to be the
angle that our Heading Angle must deviate from the DesiredCourse
to correct for the effect the the Wind is having on our aircraft.
The Sine Rule in trigonometry says that lengths of
the sides of a triangle are in the same proportion as the sine of the angles
opposite those sides. I.e. If one side is twice as long as another, the
sine of the angle opposite the longer side will be twice as large as the
sine of the angle opposite the shorter side. For our triangle this implies that : Sin(wca)/windspeed
= sin(WTAngle)/airspeed
which leads to the above equation .
Heading
Heading:=DesiredCourse+WCA;
By definition the Wind Correction Angle is the angle between the Heading and
the Desired Course: WCA = Heading - DesiredCourse which leads
directly to the above equation.
Groundspeed
groundspeed = airspeed*cos(WCA) + windspeed*cos(WTAngle)
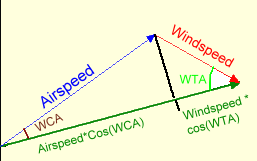
We'll use the definition of Cosine (Cosine=adjacent
side/hypotenuse) to calculate the length of the groundspeed vector. By
dropping an altitude from the vertex opposite the course side, we can divide
our Wind triangle into two right triangles as shown here. The sum
of the two adjacent pieces is the groundspeed.
We also have enough information to use the Sine Rule or
the Cosine Rule to calculate groundspeed. All three methods produce the
same answer, but the equation used here is slightly less
cumbersome.
Addendum: October 13, 2006: Since
publishing the Wind Triangle program in February, 2005, I have had
several pilots inquire about implementing an Excel spreadsheet version.
The typical problem they had was not realizing that the trig functions
require angles to be specified in radians instead of degrees.
(Also true in Delphi and most other languages.) Patrick C. recently
sent his "Flight Planning Worksheet" Excel file and I
fixed his calculation for True Heading and Ground Speed..
With his kind permission, I decided to make it available for downloading as
a prototype for the next pilot working on the problem. Patrick
lives in New Zealand (and flies a Cessna). They measure fuel in
liters and, at least in his spreadsheet, distance and speed in nautical
miles and knots. The fuel, speed, and distance calculations
would not change for other measurement systems.
Addendum February 10, 2010: An option was added
today allowing users to change the colors used for text backgrounds and
fonts, and for plotting the Wind Triangle vectors. Some of
my original color choices are made it difficult for those who are color
blind to use the program.
Running/Exploring the Program
Download source code
Download executable
Download Excel
Flight Planning Worksheet
