
Search

As of October, 2016, Embarcadero is offering a free release
of Delphi (Delphi
10.1 Berlin Starter Edition ). There
are a few restrictions, but it is a welcome step toward making
more programmers aware of the joys of Delphi. They do say
"Offer may be withdrawn at any time", so don't delay if you want
to check it out. Please use the
feedback link to let
me know if the link stops working.

Support DFF - Shop
If you shop at Amazon anyway, consider
using this link.
We receive a few cents from each
purchase. Thanks

Support DFF - Donate
If you benefit from the website, in terms of
knowledge, entertainment value, or something otherwise useful,
consider making a donation via PayPal to help defray the
costs. (No PayPal account necessary to donate via credit
card.) Transaction is secure.

Mensa®
Daily Puzzlers
For over 15 years
Mensa Page-A-Day calendars have provided several puzzles a year
for my programming pleasure. Coding "solvers" is most fun,
but many programs also allow user solving, convenient for "fill
in the blanks" type. Below are Amazon links to the
two most recent years.
Mensa®
365 Puzzlers Calendar 2017
Mensa®
365 Puzzlers Calendar 2018

(Hint: If you can
wait, current year calendars are usually on sale in January.)

Contact
Feedback:
Send an
e-mail with your comments about this program (or anything else).

|
| |
Poblem Description
Given the twenty five
numbers. 1,1,2,2,2,2,2,3,3,3,3,3,3,4,5,5,5,5,6,6,6,6,6,7,9, arrange them in a
5x5 grid in such a way that each horizontal row, vertical column and the
two main diagonals all sum to 20.
Background & Techniques
Here's a puzzle sent to me by a viewer who says it is from a set of questions
written by inventor and computer pioneer Clive Sinclair and published as "Mensa
Steps" in a magazine, perhaps "Design Technology" in 1984.
I have no idea how this puzzle would be solved with pencil and paper. I call it
"special" because the standard Magic Square definition requires that
consecutive integers from 1 to N2 be used to fill an N x N grid.
There is a vast amount of information about magic squares on the web, (11,500
Google hits for "5x5 Magic Squares"), so the solution to this one may be out there
somewhere but I did not find it.
My program solves the program in the same way that a very fast human might do
it. I divided the solution search into 3 phases.:
Phase 1
First we find all 5 number subsets of the given 25 which sum to 20. Each
row, column or diagonal must be one of these sets arranged in some order. There
are more than 50,000 was to choose 5 numbers from 25 but most of them do not sum to 20
and, of those that do, many are duplicates because of the repeated values
in the input set. When we are done filtering there are only 30
unique sets to choose from. Every row and every column (as well as the two main
diagonals), must consist of one of these 30 sets arranged in some order.
The "in some order" part though means that there can be up 120 arrangements
(permutations) of the 5 numbers. For the set {2,3,4,5,6}, the first number
can be any of the 5, the second can be any of the other 4, etc. so there are 5x
4 x 3 x 2 x 1= 120 arrangements. Repeated numbers wit in the set reduce
the number of choices. sot there may only be 30 or 60permutations for some sets -
still a lot of checking. though.
Phase 2
Phase 2 applies the other constraint that all 25 of the given numbers must
be used any set of 5 rows or columns chosen from the Phase 1 results.
Phase 2 assembles potential full grids by building 5 groups of the Phase 1
"columns" which contain the
correct number of each digit value Two "1"s, five "2"s , six
"3"s, etc. Solutions must come
from these sets, although
each of these "columns" will likely have to be rearranged to find rows and
diagonals that sum to 20 also. Of the 142,000 ways to choose 5 of the 30 Phase 1
results, there are about 4800 which contain all of the 25 given
numbers exactly once but only 110 of these are unique..
Phase 3
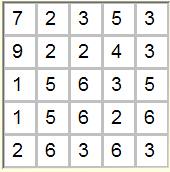 |
| One of 12 solutions from candidate column set 11279 22556
23366 23456 33356 |
We're getting closer, but not there yet. We can take any of the Phase 2
results and build 5x5 grid in which each group of 5 digits becomes a column
which sum to 20, but it is unlikely that the sums in the
other direction (the rows) will all be 20,
Phase 3 works on one of the Phase 2 results at a time. forming 5 columns and
then permuting the numbers contained in each column looking for rows which all
sum to 20. Since there are 5! (=120) ways to arrange each column, there
could be as many as 1205 (25 billion) possibilities to check.
In practice, there are many fewer than that because, again, many of the
permutations will have only 30 or 60 unique permutations because of duplicate
number values in the column. The search space is also reduced by
abandoning any solution if the row sum of the columns placed so far exceeds 20. I have not evaluated
all 110 possibilities, but in the first and last 10 groups, produced from 0 to
56
solutions each with run times per group ranging from 1 to 23 seconds. The program
does not rearrange the columns during the search, only the row positions within
each column, so there are likely hundreds or thousands more solutions than this
version finds.
Non-programmers are welcome to read on, but may want to jump to bottom of
this page to download the executable program now.
Programmer's Notes:
The program uses the TComboset class to produce the required
combinations and permutations. Recompiling will require a download of any
version of our DFF Library zip file.
To save time during searching, Phase 1 attaches a string list with all
of the unique permutations to each of the 30 potential columns and Phase 3 reads
this list rather than re-computing them each time. Phase 3 process
uses calls to recursive local function GetNextPermute to add
columns to the potential solution being tested. As each permutation
of each potential column is added, the row sums of the columns added so far is
kept and if the row sum total exceeds 20, the search for that branch is
abandoned. This was a late addition which reduced search times from
minutes to seconds for each Phase 2 line being tested.
The code is well commented and time is
short, so I'll leave this section at that for now.
Running/Exploring the Program
Suggestions for Further Explorations
 |
??? |
| |
|
| Original: March 10, 2012 |
Modified:
May 15, 2018
|
|


