Problem Description

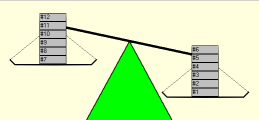You have 12 coins, one of which is counterfeit, and a balance pan scale.  The fake coin may be identified by the fact that it's weight is different from the 11 genuine coins.   Can you identify the counterfeit coin and whether it is heavier or lighter  in three weighings?

Background & Techniques

This is an old problem with lots of literature available on the web.  The best reference is probably from one of  Martin Gardner's  Mathematical Recreations columns published in  Scientific American magazine about 40 years ago.  It apparently was reprinted in book form in "Sixth Book of Mathematical Games from Scientific American"  which is unfortunately out of print.    I have copied a pretty good summary of the algorithm from the alt.rec.puzzles newsgroup  to this page: 

This program implements the Gardner algorithm to solve the problem (or check your solution) for this problem or the simpler case when you know whether the coin is heavy or light.  

To play, just select the problem type and number of coins and then drag the coins to the balance scale pans.  A weighing is recorded automatically each time the number of coins in each pan is equal so place all the coins you intend to use in one pan before loading the other pan.    When you have identified the counterfeit coin,  drag it to the answer box in the lower right corner of the form.   If you using the  "heavier or lighter" case, you'll be asked whether the coin is light or heavy to complete your solution.    A "Show me" button will display the program's solution.  

The Gardner algorithm is not very intuitive and only works for a number of coins equal to (3^W-3)/2 where W is the number of weighings required.   The program resolves this by providing you with enough spare good coins to make 12 (for the 3 weighing case).   (3³-3)/2=12.  I limited the number of coins to 12 mainly because of space to display them.  And dragging 12 coins around for the weighings is probably enough fun anyway.

Non-programmers are welcome to read on, but may want to skip to the bottom of this page to download executable version of the program.

Notes for Programmers

A TScale object descended from TImage is used to define the scale drawing methods and the animation depending on the relative weights of the pans.   An OnCountWeighing exit is used to inform the parent program when a weighing should be counted.  A weighibg is ciunted whenever the number of weights in each pan is equal.   I moved the TScale definition stuff to a unit named U_Scale just to simplify browsing the main form unit, U_Counterfeit.

U_Counterfeit contains everything else required to let the user select problem type and number of coins,  and to drag the coins to and from the balance pans and to the answer box.   The CheckMinMoves function provided the most challenge.  It implements the Gardner algorithms and builds the  "cheat sheet" answer form, ResultsForm defined in the U_Results unit.   This form is built whenever the problem type or number of coins changes, but remains hidden until the user click the "Show me button.  

600+ lines of code in U_Counterfeit and 300+ lines  in U_Scale are enough to put this well into the Advanced category, but aside from CheckMinMoves, nothing is very complex, just a lot of it.  

Running/Exploring the Program 

• Browse source extract
• Download source
• Download  executable

Suggestions for Further Explorations

	One other variation of the Counterfeit Coin problem is not implemented here - the case where we don't know if the bad coin is heavy or light, but we only need to identify it  and  not whether it is heavy or light.
	Program solutions could be animated when the user clicks the "Show me" button with coins moving to the pans as required for each weighing.
	There should be a way to solve the original problem  in three weighings without requiring the spare good coins when we have 4 through 11 coins.   But I don't know what that method is.    If anyone does, please let me know.