Problem Description
Here is a classic problem which describes how to
estimate Pi by dropping needles on a grid of parallel lines and counting
what fraction cross a line. .
Background & Techniques
I wrote the basic version of this program a couple of years ago.
It ran and I believed the results, but never felt that I really understood
the math behind it. I ran across it in my "Future
Projects" file recently and decided to understand it or throw it
out. As any teacher will tell you, the best way to test if you understand a
topic is to explain it to someone else, so here goes.
There are many Java Applets illustrating the dropping process
and some sites that explain why it works but even as a math major my
pulse still jumps a little and I flashback to college Calculus when I see
that Integral symbol. So here's my presentation and
explanation without an integral in sight (well, just one).
 It stands to
reason that if you drop a bunch of 1" needles on a sheet of paper
that has lines 1" inch part, some will cross a line and some will
not. Whether or not it crosses depends on two things, the angle of
the needle in relation to the lines and where some reference point (like
one end or the middle) is located. Here's a diagram with 1000
simulated dropped needles, of which 636 cross a line. And that 636
out of 1,000 is somehow related to Pi.
It stands to
reason that if you drop a bunch of 1" needles on a sheet of paper
that has lines 1" inch part, some will cross a line and some will
not. Whether or not it crosses depends on two things, the angle of
the needle in relation to the lines and where some reference point (like
one end or the middle) is located. Here's a diagram with 1000
simulated dropped needles, of which 636 cross a line. And that 636
out of 1,000 is somehow related to Pi.
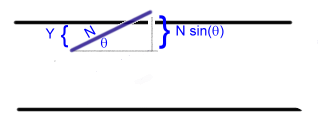 We'll look
at more experimental results later, but first here's an analytical
approach. A diagram of at a single needle the same length as
the spacing between lines might look like this. Let's call the
spacing and needle length N and make the leftmost end the
point of reference. Half the time the other end would be
higher than the left end and half the time it would be lower.
The same analysis would apply to either case. Here we'll analyze the
probability of crossing for the first case. If q
(theta) is the angle of the needle to relative to the
grid lines, then by the definition of the sine function, the right
needle end is N sine (q)
above the left end. Let Y be the distance from the line to
the left needle end. Then the needle crosses the line if Y is
less than N sine(q).
Y can vary from 0 to N and q
can vary from 0 to Pi. If we plot Y
vs. q
then the crossing cases are all points in the area under the N sine(q)
curve. For
(uniformly distributed) random Y and q,
the probability of the needle crossing is exactly the area under the curve
divided by the total area inside of the plot rectangle. The area of
the rectangle is N·Pi and the area under the curve is the definite
integral of N sine(q)
from 0 to Pi which a trigonometry book (or
web page) will tell you is N(-(cos(Pi)-(-cos(0)) =N( - ( -1 ) - (
-1 )) = 2N. So the probability, p, of needles
crossing grid lines when the needle length and spacing are identical
is p = 2N / (N·Pi) = 2 / Pi = 0.6636, roughly 2/3.
Or, if we have an estimate of p, we can solve for Pi
and get Pi = 2 / p. That's what this and most all other
program versions of the problem do.
We'll look
at more experimental results later, but first here's an analytical
approach. A diagram of at a single needle the same length as
the spacing between lines might look like this. Let's call the
spacing and needle length N and make the leftmost end the
point of reference. Half the time the other end would be
higher than the left end and half the time it would be lower.
The same analysis would apply to either case. Here we'll analyze the
probability of crossing for the first case. If q
(theta) is the angle of the needle to relative to the
grid lines, then by the definition of the sine function, the right
needle end is N sine (q)
above the left end. Let Y be the distance from the line to
the left needle end. Then the needle crosses the line if Y is
less than N sine(q).
Y can vary from 0 to N and q
can vary from 0 to Pi. If we plot Y
vs. q
then the crossing cases are all points in the area under the N sine(q)
curve. For
(uniformly distributed) random Y and q,
the probability of the needle crossing is exactly the area under the curve
divided by the total area inside of the plot rectangle. The area of
the rectangle is N·Pi and the area under the curve is the definite
integral of N sine(q)
from 0 to Pi which a trigonometry book (or
web page) will tell you is N(-(cos(Pi)-(-cos(0)) =N( - ( -1 ) - (
-1 )) = 2N. So the probability, p, of needles
crossing grid lines when the needle length and spacing are identical
is p = 2N / (N·Pi) = 2 / Pi = 0.6636, roughly 2/3.
Or, if we have an estimate of p, we can solve for Pi
and get Pi = 2 / p. That's what this and most all other
program versions of the problem do.
By the way, a much simpler application of the same concept throws darts
at a square with an inscribed circle. If the square is 2r on
a side, the probability of hitting the circle is circle area divided by
square area: p = Pi·r2 / 4r2 =
Pi / 4.
Or given our estimate for p, Pi=4p=4·(circle hits /
total darts thrown). I thought that sounded
familiar. Just found my
version of this program posted several years ago.
I didn't (or maybe couldn't) calculate the analytical case when needle
length is not equal to spacing, The adjustment I found elsewhere
makes sense - if the spacing were increased to twice needle length, the
number of crossings would logically be cut in half. If needle length
were then doubled, the number of crossings would double - so to get
numbers comparable to the "length = spacing" case we need to
multiply the observed numbers by the spacing/needle length ratio.
There's a complication in cases where the needle length exceeds the
spacing since a needle may cross two or more lines. I
allowed needle lengths up to twice spacing and counted all crossings in my
program, and results seem accurate.
We can look a histograms or crossings vs. needle angle to see how
crossings are distributed by angle. Here's the one for 1000 needles
case. For 636 crossings, this case produced an estimate for Pi
of 2/(0.636)=3.144 (This is a lot better than the
results from most 1000 needle trials, but I wanted a nice looking
histogram.)
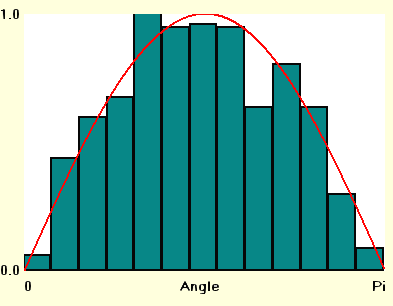 It looks
reasonable - samples with angles near 0 and 180 degrees have few
crossings, those near 90 degrees have the most crossings. Because of
the width of my chart and small number of samples, I rolled 28 degrees
worth of samples into each rectangle. I scaled the data to run from 0 to 1 in height and
overlaid the sine
function - the red curve on the chart. What if we do the same thing with more needles?
Below are typical 100,000 and 1,000,000 needle histograms.
Rectangle width for these cases was reduced to 1 pixel.
It looks
reasonable - samples with angles near 0 and 180 degrees have few
crossings, those near 90 degrees have the most crossings. Because of
the width of my chart and small number of samples, I rolled 28 degrees
worth of samples into each rectangle. I scaled the data to run from 0 to 1 in height and
overlaid the sine
function - the red curve on the chart. What if we do the same thing with more needles?
Below are typical 100,000 and 1,000,000 needle histograms.
Rectangle width for these cases was reduced to 1 pixel.

