Problem Description
This program will try to find optimal solutions for what
is commonly known as the 1-dimensional Cutting Stock Problem, The
Cutting Stock problem requires that we find the best (cheapest) way to cut
one-dimensional stock pieces (pipe, dimensional lumber, wire, rolls of paper
or other sheet material to be slit, etc.) in such a way that a given number
of pieces of specified
lengths or widths are created.
Background & Techniques
I ran across this problem via feedback from viewers wondering if my
Cutlist program would work for cutting stock to specified lengths. It
will not. However there is a technique known as Delayed Column
Generation for efficiently solving the problem. Solutions are not
perfect in the sense that extra pieces of the required lengths are not
counted as waste.
Program Usage
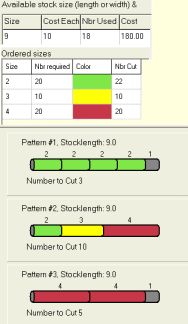
The program takes two types of data as input, Parts
and Stock: The "Solve" button finds the lowest cost way to cut the required
material. Results are displayed in text and graphical form. Check boxes
specify whether the text version of fractional and/or integer solutions are
displayed. The fractional solution assumes that unused "waste" has value.
I.E. fractional stock pieces left over are not charged to the coast. In the
integer solution, any piece cut from a stock piece results in a charge for
the entire stock piece. There is also a "Verbose" checkbox used for
debugging which displays information about intermediate results. The
graphical integer solution is always displayed.
The "Parts" grid reflects the desired output part defined by part lengths
and the number of each part length required. "Stock" input defines the
lengths of stock material required and the cost of each length. Enter
data by clicking on a row of data and entering new values. There should
always be a blank line for entering a new row of data. If not, the "Insert"
keyboard key will create one. The "Delete" key will delete any selected row.
For the Parts list, the system defines a random default color of that length
for the graphical display. Click on any color in the Parts grid to bring a
dialog where color may be changed to your preference.
Cases may be saved and restored using "Save" and "Load" buttons. Cases
are saved in text format and include the solution if the case has been
solved. Printing a saved case file is an easy way to obtain a printout of
the problem and solution.
I you're not interested in the math or programmer
notes, click here to skip to the bottom of this page to download
executable version of the program.
The Math
This is an LP (Linear programming) problem with the complication that the
number of different ways to cut
each stock piece grows exponentially with the number of lengths required and
may get too large for
traditional LP techniques. The different lengths required are rows of the
solution matrix and the unique
cutting patterns are the columns. The intersections of the input matrix
contain the number of that length
(row) which can be cut from that pattern (column). Since there may be
hundreds (or thousands or
millions) of columns, they cannot all be generated. The solution uses a
technique called "Delayed Column
Generation". Here we generate enough columns to define a solution, usually
not the optimal one. Specifically, for each part length, cut as many as
possible of that length from the longest available stock piece) until enough
parts have been cut.. That solution is used as input to the second part of
the algorithm, a "Knapsack" algorithm, which searches for an unused pattern
that improves the solution, i.e. reduces the total cost. Since the Knapsack
algorithm maximizes the value of goods that can be collected in a knapsack
of a given size, the trick here is use the "dual variables" of the LP
problem to maximize the amount of material cut per unit cost. This
process continues, swapping in each pattern which lowers the cost until no
such pattern is found.
The solution produced by the above
process is "fractional". It minimizes the total cost with the
implicit assumption that extra parts produced by a particular
pattern can be utilized and are and are not
"waste". These
Argonne National Laboratories pages provide the most
referenced and best problem description I have found.
The final step in the process attempts to convert this to an integer solution
where costs are accumulated for entire stock pieces, i.e. the customer would
pay for all of the stock that has any part cut from it. The fractional
solution provides a lower bound for the cost. Commercials
programs will do a better job of this and/or may also satisfy other
constraints such as minimizing the number of knife changes required to
producew the parts.
Non-programmers are welcome to read on, but may
want to skip to the bottom of this page to download
executable version of the program.
Notes for Programmer's
The code was adapted to Delphi code
from a Pascal version published several years ago by a
group of Korean students working under Professor Soondal Park.
Follow
this link to find the original code. I wish I could say that I
fully understood every step of the code, but my mother taught me
never to lie. :>)
I replaced static arrays to dynamic, making them one position
longer than necessary so that index values remain relative to 1 as
in the original code. I also moved the code to a separate unit (UDelayedColumnGenration)
and made a separate TCaseRec record to contain the fields
that I needed to access in the U_CutStock unit which calls
the original solution code but need access to the results for
finding the Integer solution and creating the results displays.
The section of the code which generates the integer solution from
the fractional solution is original by me. I am not sure that the
method I use guarantees an optimal solution. It assumes that no new
patterns will be introduced in moving from fractional to integer
solutions, which I have not seen proven, or even stated in my
reading so far. The specific technique I used was round each fractional
stock piece up to the next higher integer. The fractional
solution defines a lower bound for the cost; those values rounded up
provide an upper bound, but may add too much to the cost.
I recursively
remove a stock piece from of each pattern, one at a time, until the original order
quantities are not met.
As usual, bug
reports, comments, and suggestions are welcome.
Addendum April 29, 2007: The first
bug fix was posted today. Although I thought that fractional
stock and part lengths were handled correctly, they were not. The code
which determines which pattern to select next (the Dynamic Knapsack
procedure) is deeply dependent on the lengths being integers. Until I
find a replacement, my work-around is to scale the the lengths up by 10 or
100 (for 1 or 2 decimal accuracy) as necessary, solve the problem, and then
scale the results back to the original fractional values. A new
case, Kevins.txt, with non-integer part lengths was added to the test cases
in the zip files.
Addendum August 19, 2008: A while ago, a user submitted a case
that Cutstock could not solve. It has many part lengths (19) and a wide
range of lengths (134 to 6004). Today's update, Cutstock3,
allows that case (SortTest.txt) to run by sorting the input stock in
decreasing stock length before solving. The base code for this program
is not mine, and I'll admit that I have a difficult time debugging it, but I
did notice that the other test cases were presorted and sorting this case
allows a solution. I also modified the cutting
pattern graphic display to omit displaying length values when there is not
enough space (for example, many adjacent short lengths cut from long stock).
This is one of three or four programs on DFF that needs a month dedicated
to understanding and improving it, (but this this not the month
J).
Addendum September 25, 2008: One more step towards
understanding and possibly improving the search for optimum integer
solutions. A "Manual Cutting Stock" program posted today allows users
to select which patterns (and how many) to use in producing the required
number of parts. The idea of course is to produce the parts with
minimum cost. So far I have been able to match the original
program solutions some of the time, but usually not. Both "Manual
Cutting Stock" and the original "Cutting Stock" programs will read and
create case files that ate compatible with the other. It might
be the basis for a challenging new puzzle game!
November 11, 2010: Version 4 posted today fixes a problem
with part lengths that are not whole numbers. Even though the code was
modified in 2007 to handle such lengths, all the test files just had ".00"
added to the data. Any real fractional value was handled incorrectly.
Should be OK now. The Manual Cutting Stock program still does not
handle fractional part or stock lengths correctly.
Running/Exploring the Program

